حل تشریحی سوالات سؤالات امتحان نهایی درس ریاضیات گسسته دوازدهم دی 1401 - امتحان نهایی دی 1401

درستی یا نادرستی گزاره‌های زیر را مشخص کنید: (1)

الف) اگر $x$ یک عدد گنگ باشد، $\frac{1}{x}$ نیز عددی گنگ است.

ب) اگر $a|b+c$ آنگاه $a|b$ یا $a|c$.

پ) برای مقادیر حقیقی و ناصفر $a$ و $b$ به شرط آنکه $a+b\ne 0$ تساوی $\frac{1}{a+b}=\frac{1}{a}+\frac{1}{b}$ برقرار است.

ت) دو مربع لاتین متعامد از مرتبه 6 وجود ندارد.

در جاهای خالی عبارت‌های مناسب بنویسید. (1)

الف) حاصل $([m^2,m],m^5)$ برابر با ............ است.

ب) اگر برای دو عدد صحیح و ناصفر $a$ و $b$ داشته باشیم $(a,b)=1$، می‌گوییم $a$ و $b$ ............ هستند.

پ) یک مجموعه احاطه‌گر را که با حذف هر یک از رأس‌هایش دیگر احاطه‌گر نباشد، احاطه‌گر ............ می‌نامیم.

ت) تعداد یال‌های گراف $k_7$، برابر ............ است.

گزاره زیر را به روش بازگشتی (گزاره‌های هم‌ارز) ثابت کنید: (1)

«برای هر دو عدد حقیقی $x$ و $y$ داریم: $y^2+1\ge -2x(y+x+1)$»

اگر $a\ne 0$ عددی صحیح و دو عدد $(5m+4)$ و $(6m+5)$ بر $a$ بخش‌پذیر باشند ثابت کنید $a=\pm 1$. (1/25)

اگر $a$ و $b$ عددی صحیح و فرد باشد و در این صورت باقیمانده تقسیم عدد $(a^2+b^2+5)$ را بر 8 بیابید. (1)

باقیمانده تقسیم عدد $1!+2!+3!+4!+5!+\cdot \cdot \cdot \cdot \cdot \cdot +200!$ را بر 15 به‌دست آورید. ($!$ نماد فاکتوریل می‌باشد) (1/5)

معادله همنهشتی $4x\stackrel{6}{\equiv }10$ را در صورت امکان حل کرده و مجموعه جواب آن را به‌دست آورید. (1)

در هر مورد، عبارت صحیح را از داخل پرانتز انتخاب کنید. (2)

الف) تعداد رئوس یک گراف را (اندازه، مرتبه) می‌نامیم.

ب) گرافی را همبند می‌نامیم که بین هر دو رأس آن یک (مسیر، یال) وجود داشته باشد.

پ) اگر $G$ یک گراف $n$ رأسی باشد، مقدار $q(G)+q(\bar{G})$ برابر با ($n(n-1)$، $\frac{n(n-1)}{2}$) است.

ت) گراف $C_n$ تنها یک (دور، مسیر) $n$رأسی دارد.

گراف $G$ (شکل زیر) را در نظر بگیرید: (1/5)

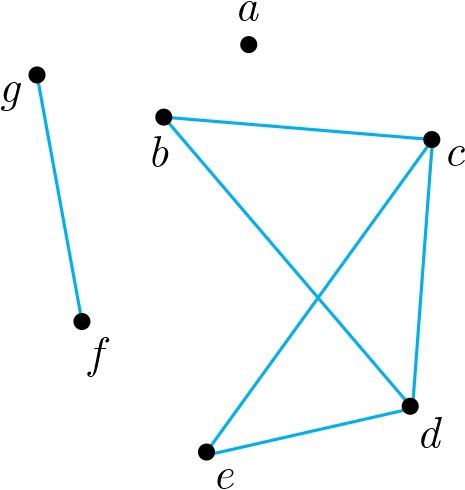
الف) $\Delta (G)$ و $\delta (G)$ را مشخص کنید.

ب) دوری به طول 4 بنویسید.

پ) دو مسیر به طول 3 با شروع از رأس $b$ بنویسید.

ت) $N_G(f)$ را با اعضا مشخص کنید.

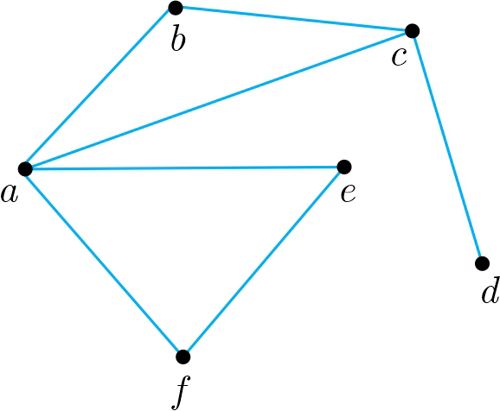
عدد احاطه‌گری را برای گراف زیر مشخص و ادعای خود را ثابت کنید. (1)

یک گراف 2-منتظم 12 رأسی بکشید که عدد احاطه‌گری آن کمترین مقدار ممکن را داشته باشد. (1)

می‌خواهیم 8 نفر را که دو به دو برادر یکدیگرند در دو طرف طول یک میز مستطیل شکل بنشانیم. اگر بخواهیم هر نفر روبه‌روی برادرش بنشیند، این کار را به چند روش می‌توان انجام داد؟ (1)

به چند روش می‌توان از بین 5 نوع گل 16 شاخه گل انتخاب کرد به‌طوری که، از گل نوع سوم فقط 3 شاخه و از گل نوع چهارم دست کم سه شاخه و از گل نوع پنجم بیش از چهار شاخه انتخاب کنیم؟ (1/75)

قرار است سه مدرس $T_3,T_2,T_1$ در سه جلسه متوالی در سه کلاس $C_3,C_2,C_1$ به‌گونه‌ای تدریس کنند که هر مدرس در هر کلاس دقیقاً یک جلسه تدریس کند. برای این منظور، با استفاده از مربع لاتین، برنامه‌ریزی کنید. (1/25)

چند عضو از مجموعه $S=\left\{n\in N|1\le n\le 630\right\}$ نه بر 3 و نه بر 5 بخش‌پذیرند؟ (1/5)

هفت نقطه درون مستطیلی به ابعاد 4 و 6 انتخاب می‌کنیم، ثابت کنید حداقل دو نقطه وجود دارد که فاصله آن‌ها کمتر از $\sqrt{8}$ است. (1/25)